En matemática, más específicamente en el cálculo infinitesimal, la
regla de l'Hôpital o
regla de l'Hôpital-Bernoulli es utilizada para determinar límites que de otra manera sería complicado calcular. La regla dice que, dadas dos funciones
f(
x) y
g(
x) continuas y derivables en
x =
c, si
f(
x) y
g(
x) tienden ambas a cero cuando
x tiende a
c, entonces el límite cuando
x tiende a
c del cociente de
f(
x) y
g(
x) es igual al límite cuando
x tiende a
c del cociente de las derivadas de
f(
x) y
g(x
), siempre que este límite exista (c
puede ser finito o infinito):
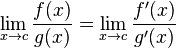
Aplicación de la regla de L'Hopital en la indeterminación
La regla de l'Hôpital se aplica para salvar indeterminaciones que resultan de reemplazar el valor numérico al llevar al límite las funciones dadas. La regla dice que, se deriva el numerador y el denominador , por separado; es decir: sean las funciones originales
f(
x)/
g(
x), al aplicar la regla se obtendrá:
f'(x)/
g'(x).


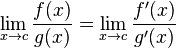
No hay comentarios:
Publicar un comentario